About Heap

Heap?

힙 이란, 데이터에서 최솟값과 최대값 을 빠르게 찾기 위해 고안된 완전 이진 트리 이다.

완전 이진 트리: 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리

힙을 사용하는 이유?

배열에 데이터를 넣고 최대 혹은 최소값을 찾으려면 O(n) 의 시간 복잡도가 필요하다. 하지만 힙에 데이터를 넣고 최대 혹은 최소값을 찾으면 O(logn) 의 시간 복잡도가 필요하다. 우선순위 큐 와 같이 최대, 최소값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현에 요긴하게 사용된다.

힙의 구조

힙은 최대 힙(최대값이 최상위) 과 최소 힙(최소값이 최상위) 으로 분류할 수 있다. 힙은 다음과 같은 두 가지 조건을 가지고 있는 자료구조이다.

• 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다.(최대힙의 경우)
• 완전 이진 트리의 형태를 가진다.

힙과 이진 탐색 트리의 공통점과 차이점

공통점

힙과 이진 탐색 트리는 모두 이진 트리 이다.

차이점

• 힙은 각 노드의 값이 자식 노드보다 크거나 같다(최대힙의 경우)
• 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 그 다음이 부모 노드, 그 다음 오른쪽 자식 노드의 값이 가장 크다.
• 이진 탐색 트리는 탐색 을 위한 구조이고, 힙은 최대/최소값 검색을 위한 구조 중의 하나이다.

힙에 데이터를 삽입하기(최대힙의 경우)

새로 삽입된 데이터가 기존의 데이터보다 클 경우, 최대힙 구조를 유지하기 위해 정렬이 필요하다.

• 새로 삽입된 데이터는 완전 이진 트리 의 구조에 맞추어, 최하단부 왼쪽 노드 부터 채워진다.
• 채워진 노드의 위치에서, 부모 노드보다 값이 클 경우, 부모 노드와 위치를 바꿔주는 작업을 반복한다.(스왑 과정)

힙에서 데이터를 삭제하기(최대힙의 경우)

일반적으로 힙에서 데이터를 삭제(뽑기) 하는 경우는 최상단의 노드가 대상이다. 따라서 일반적으로 데이터를 삭제하는 과정은 다음과 같다.

• 최상단의 데이터를 삭제한다.
• 최하단부 왼쪽의 데이터(가장 마지막 데이터)를 최상단(루트) 노드로 이동한다.
• 최상단(루트) 노드의 값이 자식 노드보다 작을 경우, 자식 노드 중 가장 큰 값을 가진 노드와 교환하는 작업(스왑)을 반복한다.

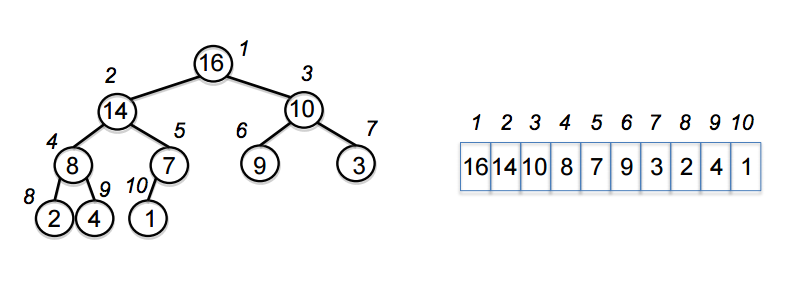
일반적인 힙의 자료구조

기본적으로 배열을 사용할 수 있다. 배열을 완전 이진 트리 라고 생각할 수 있으며, 이때 루트 노드의 인덱스는 1로 사용하는 것이 편리하다.

• 부모 노드의 인덱스 번호: 자식 노드 인덱스 번호 // 2
• 왼쪽 자식 노드의 인덱스 번호: 부모 노드 인덱스 번호 * 2
• 오른쪽 자식 노드의 인덱스 번호: 부모 노드 인덱스 번호 * 2 + 1

과 같이 표현하여 사용할 수 있다.