About Topological Sort

Topological Sort

위상 정렬은 DAG(Directed Acyclic Graph) 의 정렬로, 정점들의 선형적 순서이다.

그래프의 모든 에지 (u,v)에 대해, 정점 u는 정점 v 전의 순서에 온다.

하나의 DAG에 대한 위상 정렬은 여러개가 있을 수 있다.

위상 정렬의 첫번째 정점은 언제나 in-degree가 0인 정점이다.

TS vs DFS

DFS에서는 directed edge 를 통해 레벨이 낮은 점을 먼저 탐색한다. 하지만 이런 경우 높은 위상의 정점이 여러개 있을 때, 더 낮은 위상의 정점이 높은 위상의 정점보다 먼저 정렬 결과에 나타날 수 있다. 이 때문에 위상 정렬과 깊이 우선 탐색은 분명히 다르다.

위상정렬의 방법

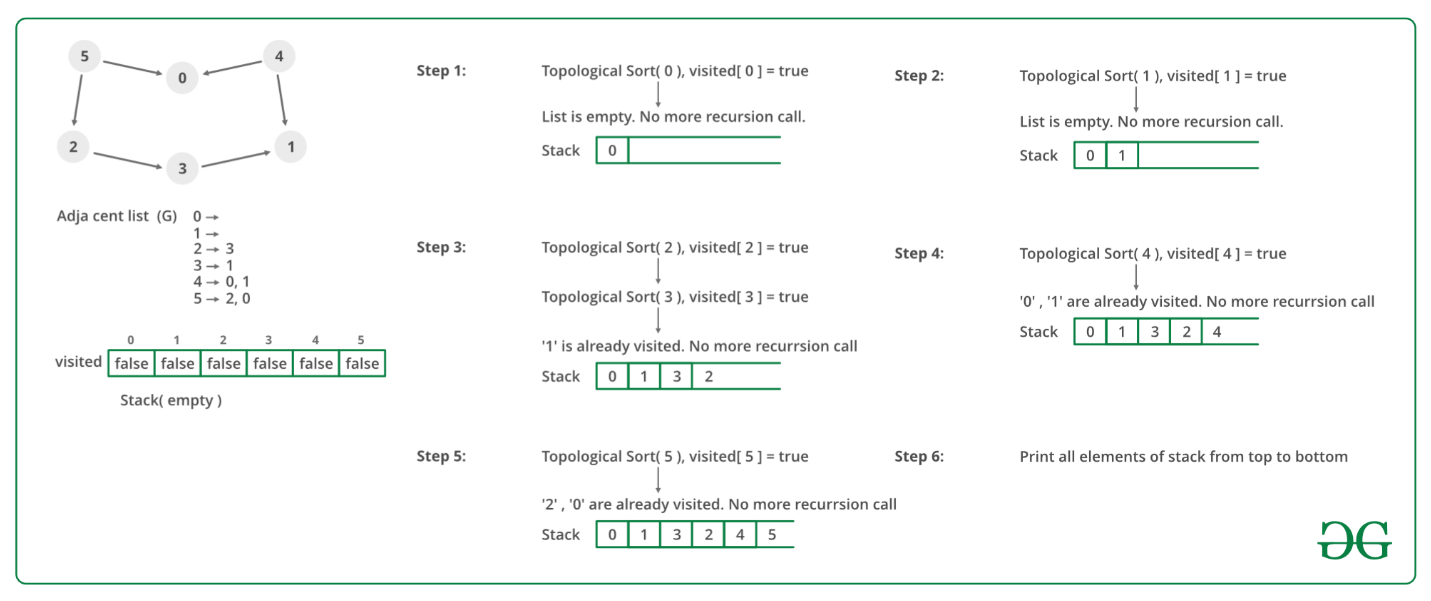
출처: Geeks for Geeks

위상 정렬에서는 스택을 사용한다. 정점을 즉시 프린트하지 않고,

1. 우선 재귀적으로 인접한 정점들에 대해 topological sorting을 call 하고,
2. 이를 스택에 넣는다.
3. 마침내 스택의 자료들을 프린트한다.

주의할점은, 정점은 해당 정점의 모든 인접한 정점들이 이미 스택에 있을 때만 스택에 추가된다는 것이다.

위상정렬의 구현

class Graph:
    def __init__(self, vertices):
        self.graph = defaultdict(list)  # dictionary containing adjacency List
        self.V = vertices  # No. of vertices

    # function to add an edge to graph
    def addEdge(self, u, v):
        self.graph[u].append(v)

    # A recursive function used by topologicalSort
    def topologicalSortUtil(self, v, visited, stack):

        # Mark the current node as visited.
        visited[v] = True

        # Recur for all the vertices adjacent to this vertex
        for i in self.graph[v]:
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)

        # Push current vertex to stack which stores result
        stack.append(v)

    # The function to do Topological Sort. It uses recursive
    # topologicalSortUtil()
    def topologicalSort(self):
        # Mark all the vertices as not visited
        visited = [False]*self.V
        stack = []

        # Call the recursive helper function to store Topological
        # Sort starting from all vertices one by one
        for i in range(self.V):
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)

        # Print contents of the stack
        print(stack[::-1])  # return list in reverse order

출처: Geeks for Geeks

Analysis

• TC: O(V+E) 스택을 추가로 이용하는 DFS와 같으므로, 시간복잡도는 DFS와 같다.
• SC: O(V) 스택을 위한 추가적인 공간이 필요하다.

위상정렬의 응용

위상정렬은 주로 job들 간의 의존도가 주어진 상태에서의 job scheduling에 사용된다.