About BFS

BFS(너비 우선 탐색)

BFS는 대표적인 그래프 탐색 알고리즘 으로, 또다른 대표적인 그래프 탐색 알고리즘 에는 DFS(깊이 우선 탐색) 이 있다.

• BFS: 정점들과 같은 레벨에 있는 노드들(형제 노드들)을 먼저 탐색하는 방식
• DFS: 정점의 자식 노드들을 먼저 탐색하는 방식

그래프의 표현 방법

HashMap 또는 Array 를 이용해서 그래프를 주로 표현함.

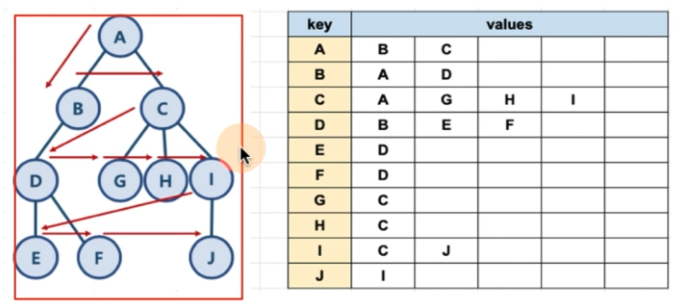
HashMap 은 키(key)와 값(value) 를 저장하는 자료구조로, 내부에서 해쉬 함수 를 통해 키 에 대한 값 을 빠르게 검색할 수 있다.

BFS 알고리즘의 구현

• HashMap: 각 노드(키)마다 연결된 노드를 배열(값)로 저장
• needVisit queue: 방문해야하는(각 노드에 연결된) 노드들을 큐로 저장
• visited queue: 이미 방문한 노드들을 큐로 저장

기본적으로 이렇게 3가지 자료구조를 활용할 수 있다.

알고리즘 순서

1. 처음 방문하는 노드를 needVisit queue에 넣은 채로 초기화한다.
2. needVist queue가 비어있지 않으면 queue에서 노드 하나를 뽑는다.
3. 뽑은 노드가 이미 방문된 노드가 아니면(visited queue에 없으면) visited queue에 넣는다.
4. 뽑은 노드와 연결된 노드들을 needVisit queue에 추가한다.
5. 다시 2번으로.

예제 코드

class BFS:
    def __init__(self):
        self.hashMap = {
            'a': ['b', 'c'],
            'b': ['a', 'd'],
            'c': ['a', 'g', 'h', 'i'],
            'd': ['b', 'e', 'f'],
            'e': ['d'],
            'f': ['d'],
            'g': ['c'],
            'h': ['c'],
            'i': ['c', 'j'],
            'j': ['i'],
            }
        self.visited = []
        self.needVisit = []

    def bfs_search(self, start_node):
        self.needVisit.append(start_node)

        while not len(self.needVisit) == 0:
            need_visit = self.needVisit.pop(0)
            if not need_visit in self.visited:
                self.visited.append(need_visit)
                self.needVisit.extend(self.hashMap[need_visit])
        print(self.visited)
        

bfs = BFS()
bfs.bfs_search('a')

시간 복잡도

일반적인 BFS의 시간 복잡도는 다음에 의존한다.

• 노드의 수: V
• 간선의 수: E 위의 구현에서 while 문은 V+E 만큼 수행된다.

따라서 시간 복잡도는 O(V + E)가 된다.